【实验目的】
加深对 FIR 数字滤波器的常用指标和设计过程的理解。
【实验内容】
针对课堂讲过的窗函数法设计线性相位 FIR 低通滤波器的例子(第七章 PPT, p57-60),利用 MATLAB 编程实现。
关于窗函数:w = rectwin(L):产生 L 点的矩形窗;w = hann(L):产生 L 点的汉宁窗;w = hamming(L):产生 L 点的海明窗;w = blackman(L):产生 L 点的 Blackman 窗;w = bartlett(L):产生 L 点的 Bartlett 窗;w = kaiser(L,beta):产生以 beta 为参数的 L点 Kaiser 窗。
[H,w] = freqz(h):产生 h 的频率响应 H 及计算相应频率响应所用的频率 w。
【实验步骤】
1、 采用窗函数法设计。
2、 用程序画出设计出的 FIR 数字低通滤波器的幅频特性曲线。
实验代码如下:
调用的函数(ideallp.m):
function my_output=ideallp(wc,N)
alpha=(N-1)/2;
n=0:1:(N-1);
m=n-alpha+eps;
my_output=sin(wc*m)./(pi*m);
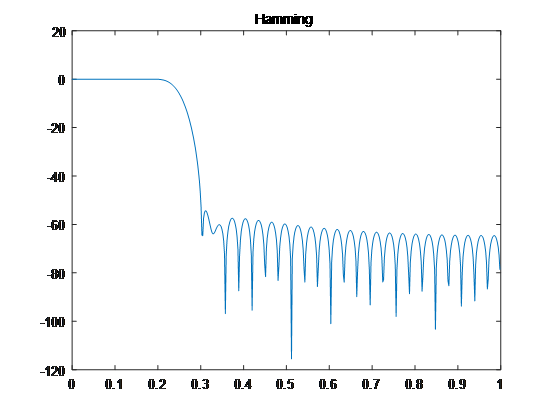
end海明窗:
wp=0.2*pi; %通带截止频率
ws=0.3*pi; %阻带截止频率
As=50; %阻带最小衰减
deltaw=ws-wp;%过渡带宽
N=ceil(6.6*pi/deltaw); %根据过渡带宽度确定N值
wdhamm=hamming(N)'; %产生N点的海明窗
wc=(wp+ws)/2; %FIR滤波器的截止频率
hd=ideallp(wc,N); %调用函数求理想的单位抽样响应
h=hd.*wdhamm; %求所设计的 FIR 滤波器的单位抽样响应
[H,w]=freqz(h,1); %计算频率响应
plot(w/pi,20*log10(abs(H)));
title('Hamming');【实验结果】
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END














- 最新
- 最热
查看全部